Estimating Mutual Information between Time Series and Temporal Event Sequences Across Diverse Analysis Tasks

Pairwise dependence measures such as correlation and causality are fundamental to temporal data mining, yet there is still no principled and robust way to quantify dependence between heterogeneous data types, especially between continuous time series and discrete temporal event sequences. Existing approaches rely on ad hoc transformations or mutual-information estimators that are highly sensitive to quantization, repeated values, and event redundancy, leading to biased or unstable results in practice. We propose a nonparametric mutual information estimator that directly measures the dependence between time series and event sequences without data transformation, learning, or ad hoc discretization. Our method models the continuous-discrete duality of real-world time series to handle quantization and repeated-value artifacts and introduces a latent event clustering strategy to mitigate bias from event co-occurrence and redundancy. Together, these yield a robust and unified framework that bridges discrete and continuous mutual information. We evaluate the proposed estimator on four representative tasks: discrete-continuous time-delayed mutual information for causality analysis, global and local temporal repetition discovery, discrete covariate selection for time series forecasting, and continuous feature selection for classification. Experiments on synthetic and real-world datasets show consistent improvements over existing methods in accuracy, robustness, and interpretability, positioning our approach as a general-purpose dependence operator for heterogeneous temporal data, similar to Pearson correlation for homogeneous time series. Code available at: https://github.com/HaojiHu/Multimodal-Temporal-Data-Quantification

CHAM-net: A Contrastive Hierarchical Adaptive Meta-network for Robust Global Methane Flux Prediction

Methane is a potent greenhouse gas that significantly contributes to global warming. However, accurately estimating global methane emissions and consumption remains challenging due to the complex interactions among environmental drivers that may vary across spatial and temporal scales. Prior data-driven methods often overlook the inherent spatiotemporal heterogeneity of ecosystems, failing to explicitly capture site-specific characteristics and cross-year evolutionary dynamics. To address these issues, we propose the Contrastive Hierarchical Adaptive Meta-network (CHAM-net), a novel framework that explicitly learns from historical context to capture site-specific dynamics. CHAM-net employs a hierarchical encoder-decoder architecture, in which the encoder captures site-specific characteristics from historical data and then dynamically conditions the decoder to generate the final prediction. Experimental results demonstrate that CHAM-net consistently outperforms all baseline methods on both simulation and observational datasets for methane emission and consumption, achieving nRMSE values as low as 0.43 and 0.88 with corresponding R2 scores up to 0.97 and 0.68 for emission prediction.

Flow Learners for PDEs: Toward a Physics-to-Physics Paradigm for Scientific Computing

Partial differential equations (PDEs) govern nearly every physical process in science and engineering, yet solving them at scale remains prohibitively expensive. Generative AI has transformed language, vision, and protein science, but learned PDE solvers have not undergone a comparable shift. Existing paradigms each capture part of the problem. Physics-informed neural networks embed residual structure, yet they are often difficult to optimize in stiff, multiscale, or large-domain regimes. Neural operators amortize across instances, yet they commonly inherit a snapshot-prediction view of solving and can degrade over long rollouts. Diffusion-based solvers model uncertainty, yet they are often built on a solver template that still centers on state regression. We argue that the core issue is the abstraction used to train learned solvers. Many models are asked to predict states, while many scientific settings require modeling how uncertainty moves through constrained dynamics. The relevant object is transport over physically admissible futures. This motivates \emph{flow learners}: models that parameterize transport vector fields and generate trajectories through integration, echoing the continuous dynamics that define PDE evolution. This physics-to-physics alignment supports continuous-time prediction, native uncertainty quantification, and new opportunities for physics-aware solver design. We explain why transport-based learning offers a stronger organizing principle for learned PDE solving and outline the research agenda that follows from this shift.

Role-Aware Conditional Inference for Spatiotemporal Ecosystem Carbon Flux Prediction

Accurate prediction of terrestrial ecosystem carbon fluxes (e.g., CO$_2$, GPP, and CH$_4$) is essential for understanding the global carbon cycle and managing its impacts. However, prediction remains challenging due to strong spatiotemporal heterogeneity: ecosystem flux responses are constrained by slowly varying regime conditions, while short-term fluctuations are driven by high-frequency dynamic forcings. Most existing learning-based approaches treat environmental covariates as a homogeneous input space, implicitly assuming a global response function, which leads to brittle generalization across heterogeneous ecosystems. In this work, we propose Role-Aware Conditional Inference (RACI), a process-informed learning framework that formulates ecosystem flux prediction as a conditional inference problem. RACI employs hierarchical temporal encoding to disentangle slow regime conditioners from fast dynamic drivers, and incorporates role-aware spatial retrieval that supplies functionally similar and geographically local context for each role. By explicitly modeling these distinct functional roles, RACI enables a model to adapt its predictions across diverse environmental regimes without training separate local models or relying on fixed spatial structures. We evaluate RACI across multiple ecosystem types (wetlands and agricultural systems), carbon fluxes (CO$_2$, GPP, CH$_4$), and data sources, including both process-based simulations and observational measurements. Across all settings, RACI consistently outperforms competitive spatiotemporal baselines, demonstrating improved accuracy and spatial generalization under pronounced environmental heterogeneity.

PEST: Physics-Enhanced Swin Transformer for 3D Turbulence Simulation

Accurate simulation of turbulent flows is fundamental to scientific and engineering applications. Direct numerical simulation (DNS) offers the highest fidelity but is computationally prohibitive, while existing data-driven alternatives struggle with stable long-horizon rollouts, physical consistency, and faithful simulation of small-scale structures. These challenges are particularly acute in three-dimensional (3D) settings, where the cubic growth of spatial degrees of freedom dramatically amplifies computational cost, memory demand, and the difficulty of capturing multi-scale interactions. To address these challenges, we propose a Physics-Enhanced Swin Transformer (PEST) for 3D turbulence simulation. PEST leverages a window-based self-attention mechanism to effectively model localized PDE interactions while maintaining computational efficiency. We introduce a frequency-domain adaptive loss that explicitly emphasizes small-scale structures, enabling more faithful simulation of high-frequency dynamics. To improve physical consistency, we incorporate Navier--Stokes residual constraints and divergence-free regularization directly into the learning objective. Extensive experiments on two representative turbulent flow configurations demonstrate that PEST achieves accurate, physically consistent, and stable autoregressive long-term simulations, outperforming existing data-driven baselines.

AgroFlux: A Spatial-Temporal Benchmark for Carbon and Nitrogen Flux Prediction in Agricultural Ecosystems

Agroecosystem, which heavily influenced by human actions and accounts for a quarter of global greenhouse gas emissions (GHGs), plays a crucial role in mitigating global climate change and securing environmental sustainability. However, we can't manage what we can't measure. Accurately quantifying the pools and fluxes in the carbon, nutrient, and water nexus of the agroecosystem is therefore essential for understanding the underlying drivers of GHG and developing effective mitigation strategies. Conventional approaches like soil sampling, process-based models, and black-box machine learning models are facing challenges such as data sparsity, high spatiotemporal heterogeneity, and complex subsurface biogeochemical and physical processes. Developing new trustworthy approaches such as AI-empowered models, will require the AI-ready benchmark dataset and outlined protocols, which unfortunately do not exist. In this work, we introduce a first-of-its-kind spatial-temporal agroecosystem GHG benchmark dataset that integrates physics-based model simulations from Ecosys and DayCent with real-world observations from eddy covariance flux towers and controlled-environment facilities. We evaluate the performance of various sequential deep learning models on carbon and nitrogen flux prediction, including LSTM-based models, temporal CNN-based model, and Transformer-based models. Furthermore, we explored transfer learning to leverage simulated data to improve the generalization of deep learning models on real-world observations. Our benchmark dataset and evaluation framework contribute to the development of more accurate and scalable AI-driven agroecosystem models, advancing our understanding of ecosystem-climate interactions.

Learning PDE Solvers with Physics and Data: A Unifying View of Physics-Informed Neural Networks and Neural Operators

Partial differential equations (PDEs) are central to scientific modeling. Modern workflows increasingly rely on learning-based components to support model reuse, inference, and integration across large computational processes. Despite the emergence of various physics-aware data-driven approaches, the field still lacks a unified perspective to uncover their relationships, limitations, and appropriate roles in scientific workflows. To this end, we propose a unifying perspective to place two dominant paradigms: Physics-Informed Neural Networks (PINNs) and Neural Operators (NOs), within a shared design space. We organize existing methods from three fundamental dimensions: what is learned, how physical structures are integrated into the learning process, and how the computational load is amortized across problem instances. In this way, many challenges can be best understood as consequences of these structural properties of learning PDEs. By analyzing advances through this unifying view, our survey aims to facilitate the development of reliable learning-based PDE solvers and catalyze a synthesis of physics and data.

Accelerating MHC-II Epitope Discovery via Multi-Scale Prediction in Antigen Presentation

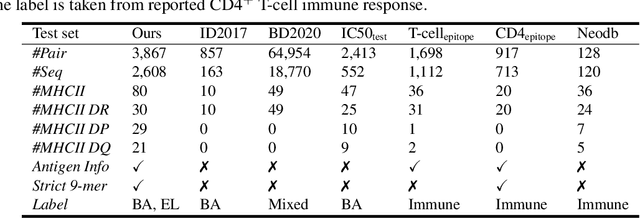
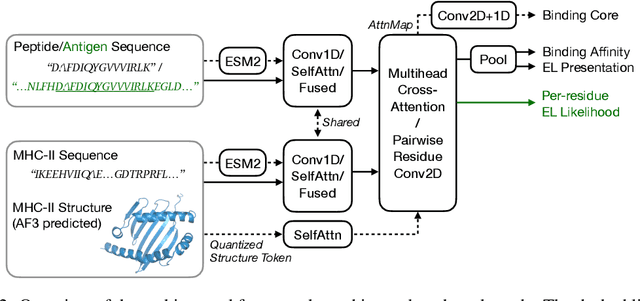
Antigenic epitope presented by major histocompatibility complex II (MHC-II) proteins plays an essential role in immunotherapy. However, compared to the more widely studied MHC-I in computational immunotherapy, the study of MHC-II antigenic epitope poses significantly more challenges due to its complex binding specificity and ambiguous motif patterns. Consequently, existing datasets for MHC-II interactions are smaller and less standardized than those available for MHC-I. To address these challenges, we present a well-curated dataset derived from the Immune Epitope Database (IEDB) and other public sources. It not only extends and standardizes existing peptide-MHC-II datasets, but also introduces a novel antigen-MHC-II dataset with richer biological context. Leveraging this dataset, we formulate three major machine learning (ML) tasks of peptide binding, peptide presentation, and antigen presentation, which progressively capture the broader biological processes within the MHC-II antigen presentation pathway. We further employ a multi-scale evaluation framework to benchmark existing models, along with a comprehensive analysis over various modeling designs to this problem with a modular framework. Overall, this work serves as a valuable resource for advancing computational immunotherapy, providing a foundation for future research in ML guided epitope discovery and predictive modeling of immune responses.

GREAT: Generalizable Representation Enhancement via Auxiliary Transformations for Zero-Shot Environmental Prediction

Environmental modeling faces critical challenges in predicting ecosystem dynamics across unmonitored regions due to limited and geographically imbalanced observation data. This challenge is compounded by spatial heterogeneity, causing models to learn spurious patterns that fit only local data. Unlike conventional domain generalization, environmental modeling must preserve invariant physical relationships and temporal coherence during augmentation. In this paper, we introduce Generalizable Representation Enhancement via Auxiliary Transformations (GREAT), a framework that effectively augments available datasets to improve predictions in completely unseen regions. GREAT guides the augmentation process to ensure that the original governing processes can be recovered from the augmented data, and the inclusion of the augmented data leads to improved model generalization. Specifically, GREAT learns transformation functions at multiple layers of neural networks to augment both raw environmental features and temporal influence. They are refined through a novel bi-level training process that constrains augmented data to preserve key patterns of the original source data. We demonstrate GREAT's effectiveness on stream temperature prediction across six ecologically diverse watersheds in the eastern U.S., each containing multiple stream segments. Experimental results show that GREAT significantly outperforms existing methods in zero-shot scenarios. This work provides a practical solution for environmental applications where comprehensive monitoring is infeasible.

Geo-Aware Models for Stream Temperature Prediction across Different Spatial Regions and Scales

Understanding environmental ecosystems is vital for the sustainable management of our planet. However,existing physics-based and data-driven models often fail to generalize to varying spatial regions and scales due to the inherent data heterogeneity presented in real environmental ecosystems. This generalization issue is further exacerbated by the limited observation samples available for model training. To address these issues, we propose Geo-STARS, a geo-aware spatio-temporal modeling framework for predicting stream water temperature across different watersheds and spatial scales. The major innovation of Geo-STARS is the introduction of geo-aware embedding, which leverages geographic information to explicitly capture shared principles and patterns across spatial regions and scales. We further integrate the geo-aware embedding into a gated spatio-temporal graph neural network. This design enables the model to learn complex spatial and temporal patterns guided by geographic and hydrological context, even with sparse or no observational data. We evaluate Geo-STARS's efficacy in predicting stream water temperature, which is a master factor for water quality. Using real-world datasets spanning 37 years across multiple watersheds along the eastern coast of the United States, Geo-STARS demonstrates its superior generalization performance across both regions and scales, outperforming state-of-the-art baselines. These results highlight the promise of Geo-STARS for scalable, data-efficient environmental monitoring and decision-making.